Frog Swap
How it works
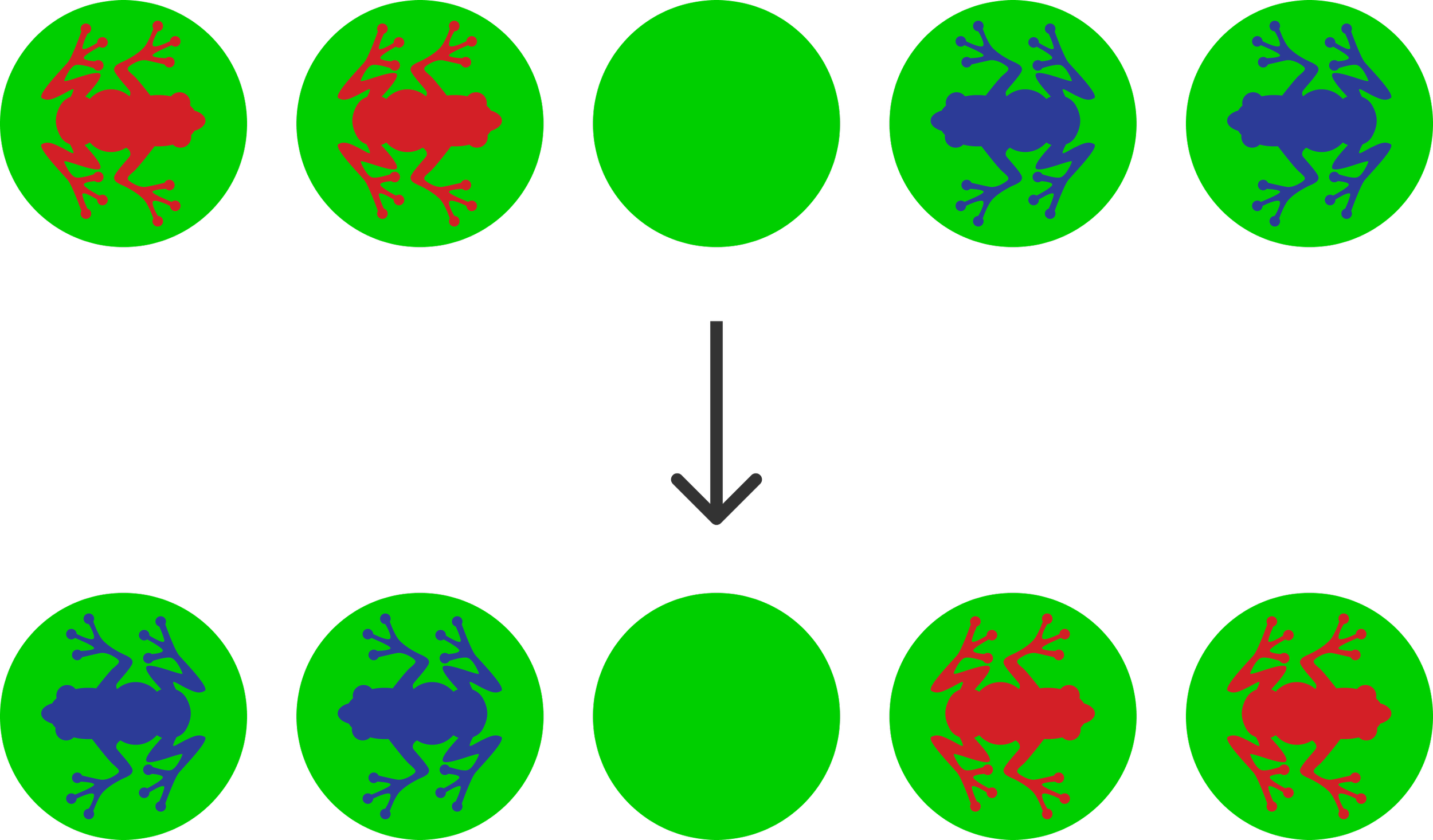
Imagine that we have 5 lily pads in a line. There are 2 red frogs on the 2 lily pads on the left and 2 blue frogs on the lily pads on the right and an empty lily pad in the middle.
The goal is to swap the red and blue frogs so that the 2 blue frogs are on the 2 lily pads on the left and the 2 red frogs are on the 2 lily pads on the right.
There are two types of moves that are allowed:
A frog can hop onto an empty lily pad that is next to it.
A frog can leap over exactly one frog of the opposite color onto an empty lily pad. (A frog can't leap over more than one frog and a frog can't leap over a frog of the same color.)
Frogs are not allowed to move backwards: Red frogs can only move to the right and blue frogs can only move to the left.
Is it possible to swap the frogs? What if there are 3 red frogs and 2 blue frogs? Or 2 red frogs and 3 blue frogs? 3 red frogs and 3 blue frogs?
In this activity, students by exploring the arrangement with 2 red frogs and 2 blue frogs. After they figure out how to swap the frogs, they explore other arrangements with different numbers of frogs and look for patterns in the numbers of hops and leaps they need in order to swap the frogs.
Why we like this activity
- It’s fun! Students enjoy the puzzle and playing with the frogs.
- It helps to develop algorithmic reasoning.
- It requires students to engage in mathematical habits of mind:
- Finding and using strategies to solve the puzzles.
- Looking for patterns / making and testing predictions / understanding and explaining when exploring how many hops and leaps each puzzle requires.
- It has a low floor and a high ceiling: Students can start exploring using trial and error, but the puzzles get more challenging as the numbers of red and blue frogs increase, and there's a lot to discover about the number of hops and leaps each puzzle requires.